これまで本欄で幾度か活用している一目均衡表。これは、市場価格の形成パターンである「波動論」、ボラティリティの傾向を計る「水準論」、時間的な傾向を判断材料とする「時間論」の3論を骨格としています。
なかでも、今回は3論の一つである「波動論」に注目してみたいと思います。これはチャート上のローソク足が描く価格変動に見られる基本的なパターンに注目したもので、すべての基本は「N波(=基本N波動」)」。つまり、チャート上に頻繁に現れる「N」字型の波形にあると考えます。
例えば、上昇波動であった場合、その基本は「上げ」→「下げ」→「上げ」の3つの波動によって構成され、仮に5波動であればNの2連続、7波動ならNの3連続などと考えるのです。この「N」が連続して現れる状態を「均衡(=比較的安定した状態)」とするならば、その「均衡」が崩れるとき、相場は転換点を迎える可能性があると考える必要が生じます。
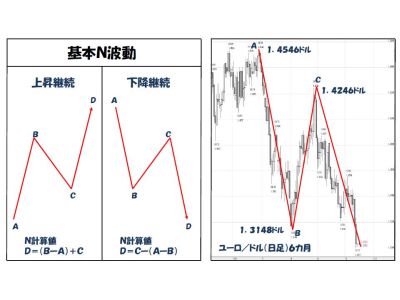
例えば、下の図(左側)で言いますと、Cの地点で切り返して上昇に向かった市場価格が過去の高値Bを上抜け、AとBの間の値幅とほぼ同じだけCから上昇することが一つの「均衡」と考えます。そうならずに、市場価格がBを上抜けることなく下降し始めたような場合は、そこで一つの転換点を迎えた可能性を考慮しなければなりません。
※ グラフをクリックいただくと拡大版をPDFファイルでご覧いただけます。
この波動論(基本N波動論)をベースに、その波動が均衡点を迎える水準を簡単な計算によって求めるのが「水準論」です。この水準というのは、目の前で形成されている波動にとって「バランスのいい水準」ということであり、実際の投資の現場では、当面の上値メドや下値メドを想定する場合に比較的よく用いられます。
上の図(右側)にあるユーロ/ドルの日足チャートを見てみると、そこにはハッキリと「N」字型の波動が形成されていることを確認することができます。執筆時の水準は過去の安値Bを下抜けており、目下のところ、その波動が徐々に「均衡点」に向かっていると想定することもできるものと思われます。
その均衡点というのは、前述したようにAとBの間の値幅とほぼ同じだけCから下降した水準と考えると、それは1.4246ドル-(1.4546ドル-1.3148ドル)=1.2848ドルという計算になります。
こうした計算によって導かれる目標値を「N計算値」と呼び、当面の上値メドや下値メドを想定する場合に用いると有効なケースが少なくありません。もちろん、ときに相場はN計算値によって求められる水準では「均衡」しないこともあり、その場合には「E計算値」や「V計算値」、「NT計算値」などを用いることもあります。それらの詳細は、また別の機会で触れることにしましょう。
コラム執筆:
田嶋 智太郎